ΦΡΟΝΤΙΣΤΗΡΙΟ ΑΛΜΑ – ΠΑΝΕΛΛΑΔΙΚΕΣ 2025 – ΣΧΟΛΙΑΣΜΟΣ ΚΑΙ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΣΗΜΕΡΙΝΩΝ ΘΕΜΑΤΩΝ 3/6/25

ΣΧΟΛΙΑΣΜΟΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΩΝ ΕΠΑΛ

Με το μάθημα των Μαθηματικών συνεχίστηκε ο αγώνας των Πανελλαδικών Εξετάσεων για τους υποψηφίους των Επαγγελματικών Λυκείων. Τα θέματα κρίνονται σαφή, κατανοητά, κάλυπταν μεγάλο μέρος της εξεταστέας ύλης αλλά και απαιτητικά αν λάβουμε υπ’όψιν μας ότι απευθύνονταν σε μαθητές Επαγγελματικών Λυκείων. Απαιτούσαν καλή προετοιμασία από μικρότερες τάξεις και μαθηματική ικανότητα. Ειδικότερα, το Θέμα Α ήταν για μαθητές που είχαν διαβάσει πολύ καλά τη θεωρία, ως και τις υποσημειώσεις του σχολικού βιβλίου. Σε γενικές γραμμές, θεωρούμε ότι οι βαθμολογίες θα κυμανθούν στα ίδια επίπεδα με τις περσινές, κρίνοντας ότι τα θέματα ήταν ανάλογης δυσκολίας.  

Ευχόμαστε σε όλους τους υποψηφίους καλή συνέχεια, επιτυχία και καλά αποτελέσματα.

ΦΡΟΝΤΙΣΤΗΡΙΟ «ΑΛΜΑ»

Αλεξανδρόπουλος Βαγγέλης

Ανδρικοπούλου Νέλλη

Βρύνας Σπύρος

Λιακόπουλος Σπύρος

Παναγιωτοπούλου Μάγδα

Aπαντήσεις μαθηματικά επαλ-2025

ΘΕΜΑ Α

Α1) απόδειξη σελίδα 93 από σχολικό βιβλίο

Α2)ορισμός σελίδα 16 από σχολικό βιβλίο

Α3)

Α)Λάθος

 Β)Σωστό

Γ)Σωστό

Δ)Σωστό

Ε)Λάθος

Α4)

α. ( c )’=0

β. (

ΘΕΜΑ Β

Β1) Ισχύει πως

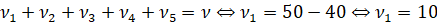
Επίσης έχουμε πως  με i=1,..,5

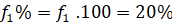
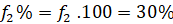
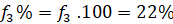
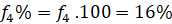
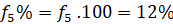
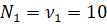
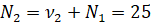
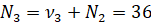
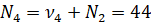
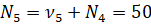
Πλήθος Ωρών	Συχνότητα	Σχετική Συχνότητα	Αθροιστική Συχνότητα
0	10	20	10
1	15	30	25
2	11	22	36
3	8	16	44
4	6	12	50
Σύνολο	50	100

Β2)

Β3) έχουμε άρτιο πλήθος παρατηρήσεων ν=50 οπότε η διάμεσος δίνεται από τον τύπο δ==

B4) α) Το πολύ τρεις ώρες υπερωριών εργάζονται το

  ποσοστό των εργαζομένων.

 Β) Με αλλαγή μεταβλητής στις προηγούμενες παρατηρήσεις μας έχουμε:

 , i=1,2,…, 50

Άρα η μέση τιμή γίνεται

ΘΕΜΑ Γ

Γ1)

, x εR

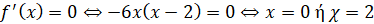
X	–∞               0                  2                       +∞
f’(x)
f(x)

                                    Ελ.               Μεγ.

H f είναι γνησίως αύξουσα στο [0,2] και γνησίως φθίνουσα στα (-∞,0]  , [2,+∞)

Γ2) Η f παρουσιάζει τοπικό ελάχιστο στη θέση χ=0 την τιμή f(0)=α

Και τοπικό μέγιστο στη θέση χ=2 την τιμή f(2)=α+8

Με δεδομένο ότι

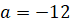
Eπομένως , x εR

Γ3) Η εφαπτομένη της f στο σημείο Μ(1,f(1))=(1,-8) είναι

με

έχουμε  ó β=-14

άρα ε: 

Γ4)Για κάθε χϵ[2,+∞) η f είναι γνησίως αύξουσα οπότε θα ισχύει

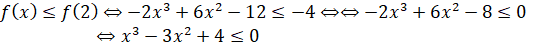
ΘΕΜΑ Δ

Δ1) Έχουμε , x εR

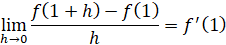
Άρα

Οπότε  από (1) 1+2λ+7=0⇔2λ=-8⇔λ=-4

Δ2)Η συνάρτηση είναι  ,x εR

, x εR

Λύνουμε

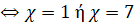
x	-∞                   1                       7                              +∞
f’(x)
f(x)

                                    Μεγ.               Ελ.

Η f είναι γνησίως αύξουσα στα διαστήματα (-∞,1] και [7,+∞)

Και γνησίως φθίνουσα στο [1,7]

Δ3) για τις τιμές 2020,2025οι οποίες ανήκουν στο [7,+∞)  με 2020<2025 και η f γνησίως αύξουσα στο [7,+∞) τότε f(2020)<f(2025)⇔0<f(2025)-f(2020)

Αντίστοιχα για τις τιμές , οι οποίες ανήκουν στο [1,7] με   και η f γνησίως φθίνουσα στο [1,7] τότε f) >f()⇔ f) -f ()>0

Επομένως ως πηλίκο θετικών όρων Α>0

Δ4)

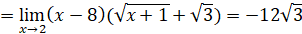
Επιμέλεια απαντήσεων

Βρύνας Σπύρος

Παναγιωτοπούλου Μάγδα

Αλεξανδρόπουλος Βαγγέλης

Ακολούθησε τα Ηλειακά Νέα στο Google News και μάθετε πρώτοι όλες τις ειδήσεις

Παρόμοια Άρθρα:

Σοβαρό τροχαίο ατύχημα στην Κάτω Αχαΐα Ξεκινούν οι εγγραφές από την Παρασκευή 10 Μαΐου για τους Παιδικους Σταθμούς Δήμου Πύργου 1ο ΓΕ.Λ. Πύργου: Εορτασμός της 11ης Πανελλήνιας Ημέρας Σχολικού Αθλητισμού την Παρασκευή 27 Σεπτεμβρίου με αθλητικές δράσεις και δραστηριότητες